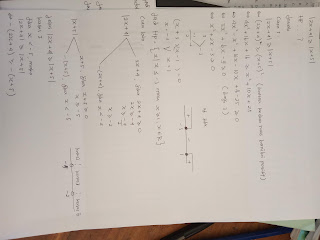
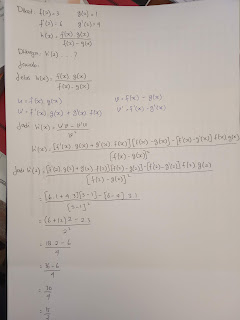Jawaban dan pembahasan soal persamaan dan pertidaksamaan rasional dan irasional

Berikut adalah jawaban dan pembahasan soal persamaan dan pertidaksamaan rasional dan irasional, materi kelas x semester 1,
Membahas tentang materi- materi matematika SMP, SMA, SMK dan contoh-contoh soal matematika beserta pembahasannya, baik soal ulangan harian, pts, maupun PAS, utbk dan lain-lain. Menyediakan juga perangkat pembelajaran baik itu rpp maupun media pembelajaran matematika