Varaibel acak dan fungsi distribusi peluang
Peluang
Misalkan A adalah suatu kejadian maka,
Dengan
Konsep variable acak
Variable acak adalah suatu fungsi yang
mengawankan suatu kejadian dari ruang sampel ke nilai numeriknya. Variable acak
dinyatakan dengan huruf besar, misalnya X, Y, dan Z, sedangkan nilai variable
acak dinyatakan dengan huruf kecil, misalnya x, y, dan z.
Variable acak ada dua macam, yaitu
variable acak diskret dan variable acak kontinu.
Variable
acak diskrit adalah variable acak yang nilai
numeriknya berupa bilangan bulat. Misalkan pada percobaan pelambungan sebuah
uang logam sebanyak dua kali. variable acak banyak diperoleh hasil gambar
adalah 0, 1, dan 2
|
Pelambungan ke 1/ pelambungan ke 2 |
A (angka) |
G (gambar) |
|
A |
AA |
AG |
|
G |
GA |
GG |
Variable acak X menyatakan banyaknya sisi
gambar yang muncul, maka:
X = 0, artinya munculnya sisi angka semua
atau tidak muncul sisi gambar
X = 1, artinya munculnya sisi gambar
sebanyak 1 kali
X = 2, artinya munculnya sisi gambar sebanyak
2 kali.
Variable
acak kontinu adalah variable acak yang nilai
numeriknya berupa interval bilangan real. Misalkan pada percobaan lama waktu
yang diperlukan siswa untuk menyelesaikan sebuah soal, variable acaknya 5 <
t < 10 dengan t menyatakan waktu dalam menit.
1.
Variable acak diskrit
Misalkan X adalah banyak nya sisi gambar yang muncul pada pelemparan sebuah uang logam sebanyak dua kali. Peluang X = 0, 1, dan 2 dari variable acak X dinamakan fungsi peluang atau fungsi kepadatan peluang nilai variable acak X (probability density function). Dinotasikan dengan f(x) atau
|
Pelambungan ke 1/ pelambungan ke 2 |
A (angka) |
G (gambar) |
|
A |
AA |
AG |
|
G |
GA |
GG |
n(S) = 4
Distribusi peluang variable acak X adalah
sebagai berikut:
|
X |
0 |
1 |
2 |
|
f(x) |
 |

|

|
Dalam notasi peluang, peluang muncul gambar kurang dari atau sama dengan satu dinyatakan dengan F(1) =
Fungsi peluang kumulatif pada X = c dinyatakan:
Sehingga distribusi peluang kumulatif
variable acak X sebagai berikut:
|
X |
0 |
1 |
2 |
|
F(X) |
 |
 |
1 |
Diperoleh dari:
F(0) =

Jika dinyatakan dalam bentuk fungsi distribusi peluang kumulatif variable acak X diperoleh sebagai berikut,
Contoh soal:
Dua buah dadu dilambungkan bersama-sama satu kali.
a.
Tentukan distribusi peluang jumlah kedua mata
dadu yang muncul
b.
Tentukan distribusi peluang kumulatif jumlah
kedua mata dadu yang muncul dalam bentuk table dan fungsi.
c.
Tentukan peluang jumlah kedua mata dadu yang
muncul sama dengan 5
d.
Tentukan peluang jumlah kedua mata dadu yang
muncul kurang dari 4
e.
Tentukan peluang jumlah kedua mata dadu yang
muncul antara 5 sampai dengan 8
f.
Tentukan peluang jumlah kedua mata dadu yang
muncul lebih dari 8
Penyelesaian:
Misalkan X = jumlah kedua mata dadu
yang muncul
a.
Pasangan jumlah kedua mata dadu yang muncul
disajikan dalam table berikut.
|
Dadu 1/ dadu 2 |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Dari table diperoleh nilai variable acak X
adalah 2,3,4,5,6,7,8,9,10,11 dan 12. Terdapat 36 pasang mata dadu sehingga n(S)
= 36. Nilai-nilai X beserta banyak anggotanya disajikan dalam table berikut:
|
Nilai X |
Banyak anggota |
|
2 |

|
|
3 |

|
|
4 |

|
|
5 |

|
|
6 |

|
|
7 |

|
|
8 |

|
|
9 |

|
|
10 |

|
|
11 |

|
|
12 |

|
Dari table dapat dihitung:
·
Peluang muncul pasang mata dadu berjumlah 2 =
f(2) = P(X=2) = 
·
Peluang muncul pasang mata dadu berjumlah 4 =
f(4) = P(X=4) = 
·
Peluang muncul pasang mata dadu berjumlah 5 =
f(5) = P(X=5) = 
·
Peluang muncul pasang mata dadu berjumlah 6 =
f(6) = P(X=6) = 
·
Peluang muncul pasang mata dadu berjumlah 7 =
f(7) = P(X=7) = 
·
Peluang muncul pasang mata dadu berjumlah 8 =
f(8) = P(X=8) = 
·
Peluang muncul pasang mata dadu berjumlah 9 =
f(9) = P(X=9) = 
·
Peluang muncul pasang mata dadu berjumlah 10 =
f(10) = P(X=10) = 
·
Peluang muncul pasang mata dadu berjumlah 11 =
f(11) = P(X=11) = 
Berdasarkan hasil perhitungan nilai-nilai
f(x) diatas dapat dibuat distribusi peluang variable acak X sebagai berikut:
|
X |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
f(x) |

|

|

|

|

|

|

|

|

|

|
|
b.
Dari table diatas diperoleh
Table distribusi peluang kumulatif variable
acak X sebagai berikut:
|
X |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
F(x) |

|

|

|

|

|

|

|

|

|
1
|
|
Fungsi peluang kumulatif variable acak X
sebagai berikut.
c. Peluang jumlah kedua mata dadu yang muncul sama dengan 5 adalah P(X = 5)
d.
Tentukan peluang jumlah kedua mata dadu yang
muncul kurang dari 4
e. Tentukan peluang jumlah kedua mata dadu yang muncul antara 5 sampai dengan 8


























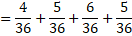





Comments
Post a Comment